|
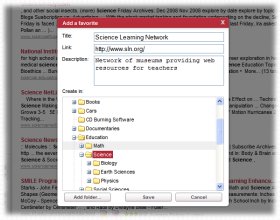
Education
Web
Viewing 1-8 of 8 total results
ψk : z 7→ zk. For which k ∈ N0 are φk, ψk immersions, submersions or embeddings. Exercise 3.7. Prove that the map φ : Rm → Cm given by φ : (x1, . . . , xm) 7→ (eix1 , . . . , eixm) is a parametrization of the m-dimensional torus Tm in Cm. Exercise 3.8. Find a...
1
0
ψk : z 7→ zk. For which k ∈ N0 are φk, ψk immersions, submersions or embeddings. Exercise 3.7. Prove that the map φ : Rm → Cm given by φ : (x1, . . . , xm) 7→ (eix1 , . . . , eixm) is a parametrization of the m-dimensional torus Tm in Cm. Exercise 3.8. Find a proof for Theorem 3.26. Exercise 3.9. Prove that the Hopf-map φ : S3 → S2 with φ : (x, y) 7→ (2xȳ, |x|2 − |y|2) is a submersion.
18
0
http://www.matematik.lu.se/matematiklu/personal/sigma/Riemann.pdf#page=18
www.matematik.lu.se/matematiklu/personal/sigma/Riemann.pdf#page=18
16 2. DIFFERENTIABLE MANIFOLDS Example 2.25. The result of Proposition 2.24 can be used to show that the following maps are all smooth. (i) φ1 : S 2 ⊂ R3 → <span class="highlight">S3</span> ⊂ R4, φ1 : (x, y, z) 7→ (x, y, z, 0), (ii) φ2 : S 3 ⊂ C2 → S2 ⊂ C×R, φ2 : (z1, z2) 7→ (2z1z̄2, |z1|2−|z2|2), (iii) φ3 : R1 → S1 ⊂ C, φ3 : t 7→ eit, (iv) φ4 : Rm+1 \ {0} → Sm, φ4 : x 7→ x/|x|, (v) φ5 : Rm+1 \ {0} → RPm, φ5 : x 7→ [x], (vi) φ6 : S m → RPm, φ6 : x 7→ [x]. In differential geometry we are especially interested in differentiable manifolds
36
0
http://www.matematik.lu.se/matematiklu/personal/sigma/Riemann.pdf#page=36
www.matematik.lu.se/matematiklu/personal/sigma/Riemann.pdf#page=36
ψk : z 7→ zk. For which k ∈ N0 are φk, ψk immersions, submersions or embeddings. Exercise 3.7. Prove that the map φ : Rm → Cm given by φ : (x1, . . . , xm) 7→ (eix1 , . . . , eixm) is a parametrization of the m-dimensional torus Tm in Cm. Exercise 3.8. Find a proof for Theorem 3.26. Exercise 3.9. Prove that the Hopf-map φ : <span class="highlight">S3</span> → S2 with φ : (x, y) 7→ (2xȳ, |x|2 − |y|2) is a submersion.
Fran�ois Edouard Anatole Lucas
also devised methods of testing primality, essentially those used today. In 1876 he used his methods to prove that the Mersenne number 2127 - 1 is prime. This remains the largest prime number discovered without the aid of a computer. The Lucas test for primes was refined by Lehmer in 1930. It work...
Stanford Encyclopedia of Philosophy: and modern physics
film is young; it has just been placed in the camera and is ready to be exposed. It is then exposed to the object that comes out of the time machine. (That object in fact is a later stage of the film itself). By the time we come to stage S2 of the life of the film, it has been developed and is about...
Asteroid Heating: A Shocking View
to 10,000 times the atmospheric pressure at the surface of the Earth. Shock Stage Effects resulting from general shock pressure Effects resulting from local P-T excursions Shock Pressure (Gpa) Minimum temp. increase (oC) S1 unshockedSharp optical extinction as viewed in microscope. Small number of...
Table of Moons
J. Kleyna22,707,00061,297.7 Suttungr2000Gladman et al.19,470,00071016.8 S/2004 S07 2004D. Jewitt, S. Sheppard, J. Kleyna19,800,00061,103 S/2004 S12 2004D. Jewitt, S. Sheppard, J. Kleyna19,650,00051,048 S/2004 S13 2004D. Jewitt, S. Sheppard, J. Kleyna18,450,0006906 S/2004 S17 2004D. Jewitt, S. Sheppa...
Stanford Encyclopedia of Philosophy: evolutionary
do well against each other. All of the other strategies involve S3, S4, R3, or R4, which results in the same act being performed no matter what the external state is. Sender Strategies: S1:Send M1 if T1; M2 if T2 S2:Send M2 if T1;M1 if T2 S3:Send M1 if T1 or T2 S4:Send M2 if T1 or T...
represent characters in familiar stories (PK-LL-S1) (ELA-1-E4) 8. Listen to a story and state orally what the story is about (PK-LL-R1) (PK-LL-R2) (PK-LL-L1) (ELA-1-E5) 9. Answer simple questions about a story read aloud (PK-LL-S3) (PK-LL-R4) (ELA-1-E5) 10. Share related life experiences afte...
1
0
represent characters in familiar stories (PK-LL-S1) (ELA-1-E4) 8. Listen to a story and state orally what the story is about (PK-LL-R1) (PK-LL-R2) (PK-LL-L1) (ELA-1-E5) 9. Answer simple questions about a story read aloud (PK-LL-S3) (PK-LL-R4) (ELA-1-E5) 10. Share related life experiences after stories are read aloud (PK-LL-L1) (PK-LL-S1) (ELA-1-E6) 11. Orally express thoughts about characters or events in a story (PK-LL-S1) (PK-LL-S2) (PKS-LL-R2) (ELA-1-E6) Standard 7: 12. Demonstrate understanding
1
0
http://www.doe.state.la.us/lde/uploads/3906.pdf#page=1
www.doe.state.la.us/lde/uploads/3906.pdf#page=1
represent characters in familiar stories (PK-LL-S1) (ELA-1-E4) 8. Listen to a story and state orally what the story is about (PK-LL-R1) (PK-LL-R2) (PK-LL-L1) (ELA-1-E5) 9. Answer simple questions about a story read aloud (PK-LL-<span class="highlight">S3</span>) (PK-LL-R4) (ELA-1-E5) 10. Share related life experiences after stories are read aloud (PK-LL-L1) (PK-LL-S1) (ELA-1-E6) 11. Orally express thoughts about characters or events in a story (PK-LL-S1) (PK-LL-S2) (PKS-LL-R2) (ELA-1-E6) Standard 7: 12. Demonstrate understanding
HIGH SCHOOL MATHEMATICS CONTENT EXPECTATIONS page 3 of 19 11/07 MICHIGAN DEPARTMENT OF EDUCATION STANDARDS (and number of core expectations in each standard) A1: Expressions, Equations, and Inequalities (16) A2: Functions (16) A3: Families of Functions (27) G1: Figures and Their Properties (29) G...
1
0
HIGH SCHOOL MATHEMATICS CONTENT EXPECTATIONS page 3 of 19 11/07 MICHIGAN DEPARTMENT OF EDUCATION STANDARDS (and number of core expectations in each standard) A1: Expressions, Equations, and Inequalities (16) A2: Functions (16) A3: Families of Functions (27) G1: Figures and Their Properties (29) G2: Relationships Between Figures (10) G3: Transformations of Figures in the Plane (5) S1: Univariate Data- Examining Distributions (9) S2: Bivariate Data— Examining Relationships (6) S3: Samples
5
0
http://www.michigan.gov/documents/Math11-14-open1_142202_7.pdf#page=5
www.michigan.gov/documents/Math11-14-open1_142202_7.pdf#page=5
HIGH SCHOOL MATHEMATICS CONTENT EXPECTATIONS page 3 of 19 11/07 MICHIGAN DEPARTMENT OF EDUCATION STANDARDS (and number of core expectations in each standard) A1: Expressions, Equations, and Inequalities (16) A2: Functions (16) A3: Families of Functions (27) G1: Figures and Their Properties (29) G2: Relationships Between Figures (10) G3: Transformations of Figures in the Plane (5) S1: Univariate Data- Examining Distributions (9) S2: Bivariate Data— Examining Relationships (6) <span class="highlight">S3</span>: Samples
|